细说经典密码学ADFG(V)X(三)
译者序
NSA文档解密 05/06/2014
这是一篇NSA文档,关于二战时期使用的ADFGVX加密系统的通解方法,原文为ADFGVX加密系统的通用解决办法,这里虽然是翻译,但主要采用意译的方式,将其中核心的部分解释出来,并加以自己的理解,希望能减轻读者的理解难度,如有必要,可以阅读原文,如有谬误,还请指正。
ADFGVX为棋盘密码+列移位(+转置)的组合,而棋盘密码本质上为替换密码。
文中提到的矩阵,指的是在经过明文消息在经过替换后,进行列移位时所创造的矩阵,详情可查看之前文章在列移位部分进行的变换。
文中提到的key,指列移位时用到的移位密钥。
文中所有的密文消息,均由同一套列移位密码和棋盘密码加密
文中提到的元素,指密文的ADFGVX六个字符,一个字符称一个元素。
原文的附录1没有在此翻译,因为附录1实际上是另一篇文章了,实在太长。
简介
ADFGVX加密算法源于二战时期的德军,该算法整合了替换和移位两种密码学算法,因为其密文中只有ADFGVX六种字符,因此被称为ADFGVX加密,在二战快要结束的时候,一共有三种针对该算法的方法,但都有一些限制,分别为
- 有两则明文开头部分相同/相似的密文
- 有两则明文结尾部分相同/相似的密文
- 有数则密文且这些密文刚好完全将矩阵填充完整
由此我们展开了一项对ADFGVX通解的研究。
此论文旨在介绍我们取得的研究成果,我们也相信该研究能够对其他的密码学工作有所启迪。
正文
讨论
这里给出的通解是基于对加密系统中使用的初始及结束时元素的频率变换分析,并在此假设棋盘没有被刻意地修改以达到元素频率均匀分布的目的。本文假定读者已经知道怎么去解密开头/结尾部分相同的ADFGVX密文。
在附录中给出了12则以相同key加密的消息以供测试。
首先,需要先确定key的长度是奇数还是偶数,也就是矩阵的列长是奇数还是偶数。
因为每个明文字母被替换成两个元素,因此可以得出两个结论:
- 当列数为偶数时:矩阵的每一行都是棋盘横坐标或纵坐标(也就是类型相同)
- 当列数为奇数时:矩阵将隔行进行横纵坐标交替变换(也就是奇数行与奇数行类型相同,偶数行与偶数行类型相同)
对于多则消息,他们的第一个元素一定是属于同一类别(或横坐标或纵坐标),因此这些元素可以合并分析,得到一个简单的频率表。引申一下,他们的第3、5等奇数位置也是和第一个元素属于同一类别的,只要他们是在矩阵的同一列中,那么这些元素也可以添加到那个频率表中。
不过为了保证这些元素在同一列中,我们应该对取得的元素数量做一个限制,具体限制应当取决于消息的大小。考虑到绝大多数情况,我们可以安全地假设转置矩阵的列数不超过25列。
此外,和奇数位词频分析相同,也可以创建一个偶数位的频率表。
如果矩阵有偶数列的话,上述两个频率表应当呈现相似的频率,如果矩阵有奇数列的话,两个频率表应当有所差异。
我们对样本数据进行了测试,如下是他们的元素频率表。

两张表产生了明显的差异--VXF在图一和图二中展现的频率明显不同,元素V和X在奇数位的频率很高,但是在偶数位频率很低,F在奇数位频率很低但是在偶数位频率却很高。
消息3和消息11每个包含了186个元素,如果他们的奇偶位是矩阵横纵坐标交替的话(也就是说第1、3、5位是奇/偶,2、4、6位是偶/奇),那么由于上述问题,VX很可能在其中一个隔行里出现(比如1 3 5或者2 4 6),而F则更可能在另一个隔行中出现(假设VX在1 3 5出现,那么F应当在2 4 6中出现)。而如果这种隔行情况在密文消息的某处被逆转了(如果前段密文VX多出现在奇数位,中间某段出现在偶数位,F相反),那么就说明了这里矩阵某一列的结束和另一列的开始。
基于这个想法,测试一下消息3 11。

在开头的前十个元素里,VX落在了奇数位上,而F落在了偶数位上;此后的十个元素中,F落在了奇数位上而VX落在了偶数位上。通过这种变化可以猜测到,矩阵的第一列在大概第10个元素左右结束。同样的变化也发生在第21~30个元素,但是这次的变化非常明显,VX同时出现在了22和23的位置,这说明22是一列的结束,而23是另一列的开始。如果列1和列2一共有22个元素,那么也就是说每一列都有11个元素,那么一共就有17列(即ceil(186/11)),而且这个矩阵的列长较短(只有11个元素)。
这里还有另一则消息也列长也比较短,即消息7,其有254个元素,(17*15)-1=254。这个消息的列长比消息3 11的列长多了4个元素,现在先假设最后一列为短列(一共有17列,有16列为长列,1列为短列),那么消息7就可以直接放在消息3和11一起分析,那么就只要考虑消息7每列后面的4个元素就可以了。


由于同样的理由,第55 56位处也有一个变化,这遵循了一个原则--前五列的列长是一样的。
这五列包含了两种类型,我们用+和-来表示,一种是横/纵坐标,另一种是纵/横坐标,我们来尝试将其区分。
对于每一列,制作一个奇数位和偶数位的频率表,以第一列为标准,如果其他列做出的某一频率表和第一列相同(奇数位和偶数位频率与其相同),那么就标记为+,如果相反,就标记为-。
由此我们发现前五列分别是+++-+。
为了区分更多的列,我们需要做更多的数学工作。因为矩阵只有17列,所以我们可以对图1 2 所示的一般频率表的频率情况进行加权处理(图1 2假设矩阵为25列),结果如下。

消息5有202个元素,有两个短列(17*12-2=202),而消息3 11 7只有一个短列,那么消息5就和这三则消息共同拥有一个短列,此外还拥有一个独立的短列,如何找到这个短列呢。
假设第一列是附加的短列,然后第二列出现的字母为FXFXFFFVAGFD,根据图五加权,得出加权后权重总值为77,而逆序为144,计算如下
将这些元素分配到不同的奇偶位上:

(译者注:这里的计算方法的主要思想应当是将奇数位x奇数位加权+偶数位x偶数位加权,以此得到其为奇-偶排序情况下的权重,同理算得偶-奇排序的权重)
那么列2就是-,但是已知列2是+,因此列1就不是短列,但是假设列2是短列就不会由这个冲突,计算如下:
假设列2是短列,那么列3就是XAVDAGFDVDGF
奇-偶频率权重为(XVAFVG 和 ADGDDF) 136
偶-奇频率权重为(ADGDDF 和 XVAFVG) 109
因此列3就是一个+列,这就和前面所述的结果--前五列顺序为+++-+是相符合的。
如果前面所有的推理过程都正确,而且列2的确是一个短列,那么这一列一定就是在正确矩阵的倒数第二列。既然这一列是+,那么最后一列一定是-,因此,一共有9个-列和8个+列,那么现在就可以确定下来了: -列是奇数列,而+列是偶数列。
消息3 11 7共有一个短列,以下为每列获得+/-的可能性列表:

如果某一列的猜想是正确的话,那么应该满足如下条件
- 9个-列和8个+列
- 短列应该是-列
只有当假设3 5,也就是8 10列为短列的时候,才符合这个条件。
因此,列2后面应当是8或者10列,测试2-8列的元素频率分布,得到如下
测试2-10列的元素频率分布,如下

显然,2-8更符合词频分布。
可以通过附加的短列来确定更多的key,如此一来,可以通过消息12和消息6来确定前散列是16-5-7。使用Anagramming技巧可以快速的解决问题。
最后得到的移位密钥如下

棋盘密码如下
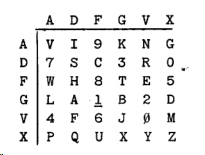
附录






