解密LockCrypt勒索软件
本文翻译自:https://researchcenter.paloaltonetworks.com/2018/07/unit42-decrypting-lockcrypt-ransomware/
LockCrypt,也叫EncryptServer2018,是2017年中发现的勒索软件家族,至今仍然活跃。网络上没有公开的LockCrypt的解密方法。恶意软件的变种已经使用了更强的加密方法,本文对旧版恶意软件的解密进行分析。
初始分析
研究人员发现恶意软件作者用一些看起来弱加密的定制加密方法来加密文件,这让研究人员很惊讶,在2018年居然遇到了勒索软件使用定制的加密模型,如果使用Windows API来加密数据的方式,那么以现在的硬件进行解密可能需要几十亿年。
对加密函数的分解与下面的python代码是等价的:
def grouper(iterable, n, fillvalue=None):
"""returns a generator which iterates iterable in groups of size n.
in case the last group is incomplete, it is padded with fillvalue"""
args = [iter(iterable)] * n
return itertools.izip_longest(fillvalue=fillvalue, *args)
def rol(val, n, width):
"""equivalent to the x86 rol opcode"""
return (val << n) & ((1<<width)-1) | \
((val & ((1<<width)-1)) >> (width-n))
def encrypt(key, plain):
size = len(plain)-2
enc = io.BytesIO(plain)
# phase 1
key_cyclic = grouper(itertools.cycle(key), 4)
for _ in xrange(0, size&(~0x3), 2): # align the size of the data to a multiple of 4 bytes
# get the next key dword
k = "".join(key_cyclic.next())
k = struct.unpack("<I", k)[0]
# get the next data dword
d = enc.read(4)
d = struct.unpack("<I", d)[0]
# XOR them and put it back to the data
e = k^d
e = struct.pack("<I", e)
enc.seek(-4, os.SEEK_CUR)
enc.write(e)
# go back 2 bytes in the data stream (so that loop iterations overlap)
enc.seek(-2, os.SEEK_CUR)
# phase 2
enc.seek(0, os.SEEK_SET)
key_cyclic = grouper(itertools.cycle(key), 4)
for i in xrange(0, size&(~0x3), 4):
# get the next key dword
k = "".join(key_cyclic.next())
k = struct.unpack("<I", k)[0]
# get the next data dword
d = enc.read(4)
d = struct.unpack("<I", d)[0]
# rotate the data dword
e = rol(d, 5, 32)
# XOR it with the key dword
e = e^k
# swap the byte order
e = struct.pack(">I", e)
# put the data dword back
enc.seek(-4, os.SEEK_CUR)
enc.write(e)
return enc.getvalue()
def encrypt_file(key, file):
# len(key) == 25000
# leave the first 4 bytes as-is
file.seek(4, os.SEEK_SET)
# encrypt the rest of the first 1MB of the file
plain_data = file.read(0x100000 - 4)
enc_data = encrypt(key, plain_data)
file.seek(4, os.SEEK_SET)
file.write(enc_data)
# leave the rest of the file as is
下面的结论是等价的:
- phase 1定义的转化是一个长度为12500字节的循环;
- phase 2定义的转化是一个长度为25000字节的循环;
- 除了边缘情况,每个明文位要与3个密钥位进行XOR运算;
- 如果在phase 2对位移操作undo(撤销),phase 1和2都可以描述为用长度为25000字节的循环密钥进行的流加密。
最后2个结论可以通过下面的转化图进行说明,⊕表示进行XOR操作。
在转化之前,4:8字节的位是这样的:

Phase 1的第2轮循环之后:

Phase 1的第3轮循环之后:

Phase 1的第4轮循环之后(与整个phase 1的循环相同):
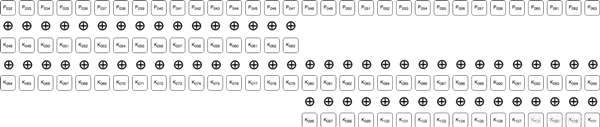
Phase 2的第2轮循环进行ROL(循环左移)操作之后:

Phase 2的第2轮循环进行XOR操作之后:

字节的顺序交换完成,这也就是这些字节的加密过程。
恢复stream key
如果从上图中拿到加密后的4:8字节,对交换顺序进行逆操作,ROR(循环左移)5位,就得到:

上面的操作是将加密进行标准化,变成一个典型的流加密。如果再对这些字节用已知的明文字节进行XOR运算,就得到结论4中提到的密钥位的功能:
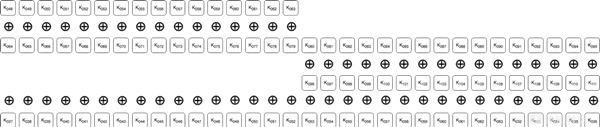
该流被称之为stream key(流密钥),而流中的每一位都是对原始密钥的位进行了三次XOR运算。因为是一个长为25000字节的循环,因此要恢复并解密加密的文件,需要25000字节的明文和加密字节。
下面的python函数可以用给定的明文和加密的数据对恢复stream key。索引参数指定了给定字符串(减去4,因为前4个字节是不加密的)中的25000已知明文字节的索引,比如只会用到明文字符串的字节idx+4:idx+4+25000。
key_len = 25000
def ror(val, n, width):
return ((val & ((1<<width)-1)) >> n) | \
(val << (width-n) & ((1<<width)-1))
def recover_stream_key(plain, enc, idx):
assert len(plain) == len(enc)
assert len(plain) >= 4 + idx + key_len
plain = io.BytesIO(plain)
enc = io.BytesIO(enc)
assert plain.read(4) == enc.read(4)
plain.seek(idx & (~3), os.SEEK_CUR)
enc.seek(idx & (~3), os.SEEK_CUR)
stream_key = io.BytesIO()
for i in xrange(0, key_len + (idx % 4), 4):
# read the next plain dword
p = plain.read(4)
p = struct.unpack("<I", p)[0]
# read the next encrypted dword and undo the bit shifts on it
e = enc.read(4)
# unswap the byte order
e = struct.unpack(">I", e)[0]
# ROR back 5 bits
e = ror(e, 5, 32)
# XOR the plain and normalized encrypted dwords
k = p^e
k = struct.pack("<I", k)
# write the stream key dword to the recovered stream key stream
if i == 0:
stream_key.write(k[idx % 4:])
elif i < key_len:
stream_key.write(k)
else: # i == key_len
stream_key.write(k[:-idx % 4])
stream_key = stream_key.getvalue()
assert len(stream_key) == key_len
return stream_key
然后用下面的函数来解密文件:
def decrypt(stream_key, enc):
size = len(enc) - 2
plain = io.BytesIO(enc)
stream_key_cyclic = grouper(itertools.cycle(stream_key), 4)
for i in xrange(0, size&(~3), 4):
# read the next stream key dword
sk = "".join(stream_key_cyclic.next())
sk = struct.unpack("<I", sk)[0]
# read the next encrypted dword and undo the bit shifts on it
e = plain.read(4)
# unswap the byte order
e = struct.unpack(">I", e)[0]
# ROR back 5 bits
e = ror(e, 5, 32)
# XOR the normalized encrypted dword with the stream key dword to recover
# the plain dword
p = e^sk
p = struct.pack("<I", p)
plain.seek(-4, os.SEEK_CUR)
plain.write(p)
return plain.getvalue()
def decrypt_file(stream_key, file):
assert len(stream_key) == key_len
# leave the first 4 bytes as-is
file.seek(4, os.SEEK_SET)
# decrypt the rest of the first 1MB of the file
enc_data = file.read(0x100000 - 4)
plain_data = decrypt(stream_key, enc_data)
file.seek(4, os.SEEK_SET)
file.write(plain_data)
# leave the rest of the file as is
前2个加密字节(原始文件的字节4:6)只与2个key位进行XOR运算,因此:
- 为了解密余下的字节,必须使用idx>=2的stream key
- 为了解密前2个字节,必须使用idx=0的stream key
如果原始文件的长度!= 2 (mod 4),那么在encrypt()函数中明文的长度len(plain) != 0 (mod 4),因此在phase 1的最后一个循环中只对文件结尾的1-2个字节进行解密。这些字节的明文位只与1 key位进行XOR运算,因为还不能解密。
如果已知文件的长度n>=m,就可以解密长为m的文件。
可以得出结论,为了能够解密任意长度的文件和文件名,需要恢复原始的解密密钥,而不仅仅是前面提到的stream key。
恢复original key
分析表明上面的线性方程组将stream key和original key联系在一起。如果尝试将分析公式化,下面的python函数可以给出original key位标记,然后位标记与stream key位进行XOR运算:
key_bitlen = 25000*8
def k_for_i(i):
i_dword = i >> 5 # the index of the dword for bit i
i_offset = i % 32 # the index of bit i in its dword
i = i + key_bitlen
k = []
k.append((i_dword << 6) + i_offset)
if i_offset < 16:
k.append(k[0] - 16)
else:
k.append(k[0] + 16)
k.append((i_dword << 5) + ((i_offset + 5) % 32))
return [x % key_bitlen for x in k if x >= 0]
stream_key[i] == reduce(xor, (key[k] for k in k_for_i(i)))有了这个函数,就可以生成一个200000×200000稀疏矩阵,描述original key和stream key之间的转化:
def gen_equations(idx):
A_i_j_s = []
for i in xrange(idx << 3, (idx << 3) + key_bitlen):
A_i_j_s.append(k_for_i(i))
return A_i_j_s矩阵A的第i行除了A_i_j_s[i]是1外,其他列元素都是0。
因此,得到的矩阵非常稀疏,每行只有3个值,所以适用于在普通电脑上用线性几何方法去解决该问题。比如,用SageMath软件:
# fix the following parameters to those of your own
stream_key_idx = 25000 # the stream key idx you recovered
stream_key_path = "key-stream-idx-25000.bin" # the path to the stream key you recovered
original_key_path = "key.bin" # the path to write the original key to
import itertools
import struct
def grouper(iterable, n, fillvalue=None):
args = [iter(iterable)] * n
return itertools.izip_longest(fillvalue=fillvalue, *args)
def str2bits(s):
bits = []
for dword in grouper(s, 4):
dword = "".join(dword)
dword = struct.unpack("<I", dword)[0]
bits += [(dword >> i) & 1 for i in xrange(32)]
return bits
def bits2str(bits):
s = []
for dword_bits in grouper(bits, 32):
dword = 0
for i, bit in enumerate(dword_bits):
dword = dword | (bit << i)
s.append(struct.pack("<I", dword))
return "".join(s)
with open(stream_key_path) as f:
stream_key = f.read()
assert len(stream_key) == 25000
stream_key_bits = str2bits(stream_key)
Y = vector(GF(2), 200000, stream_key_bits)
# create a matrix with the equations for the stream key bit
A_i_j_s = gen_equations(stream_key_idx)
A = matrix(GF(2), 200000, sparse=True)
for i, A_i_j in enumerate(A_i_j_s):
for j in A_i_j:
A[i,j] = 1
# recover the original key bits
X = A.solve_right(Y)
key_bits = [int(x) for x in X.list()]
key = bits2str(key_bits)
with open(original_key_path, 'wb') as f:
f.write(key)
解密文件
总结一下,恢复加密密钥的步骤如下:
恢复至少25010字节的未加密文件或明文文件;
- 研究任意建议先在另一台机器上安装勒索软件加密的软件(相同版本),然后比较加密DLL文件和原始文件的大小;
安装python 2.7;
用recover_stream_key.py脚本来恢复给定加密文件和明文文件中idx >= 2的stream key。
- 如果有大量已知的明文文件,研究任意建议使用idx = 25000。
安装SageMath;
打开SageMath Jupyter Notebook,复制并执行上面的代码段来恢复原始的加密密钥;
- 从实验的结果看,这一步需要花费20分钟到几个小时
使用decryptor.py脚本来解密加密的文件;
脚本下载地址为Unit 42的GitHub:https://github.com/pan-unit42/public_tools/tree/master/lockcrypt