Crypto-RSA-公钥攻击小结
前言
本篇文章对一些常见的公钥RSA攻击进行小结,欢迎补充
e=1
当e只有1的时候,我们有
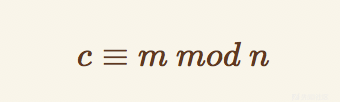
当c小于N的时候,c即m
题目如下
N=0x180be86dc898a3c3a710e52b31de460f8f350610bf63e6b2203c08fddad44601d96eb454a34dab7684589bc32b19eb27cffff8c07179e349ddb62898ae896f8c681796052ae1598bd41f35491175c9b60ae2260d0d4ebac05b4b6f2677a7609c2fe6194fe7b63841cec632e3a2f55d0cb09df08eacea34394ad473577dea5131552b0b30efac31c59087bfe603d2b13bed7d14967bfd489157aa01b14b4e1bd08d9b92ec0c319aeb8fedd535c56770aac95247d116d59cae2f99c3b51f43093fd39c10f93830c1ece75ee37e5fcdc5b174052eccadcadeda2f1b3a4a87184041d5c1a6a0b2eeaa3c3a1227bc27e130e67ac397b375ffe7c873e9b1c649812edcd
e=0x1
c=0x4963654354467b66616c6c735f61706172745f736f5f656173696c795f616e645f7265617373656d626c65645f736f5f63727564656c797d此时只要
print libnum.n2s(c)
即可
Rabin算法
满足条件
e=2,且n可以被分解
(既然n可以被分解,为什么不直接算d?因为不互素,没法求逆元)
通解方法
我们有

此时计算两个值

又因为gcd(p,q)=1
那么有
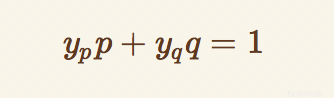
可以求出两个y,然后再计算下列4值
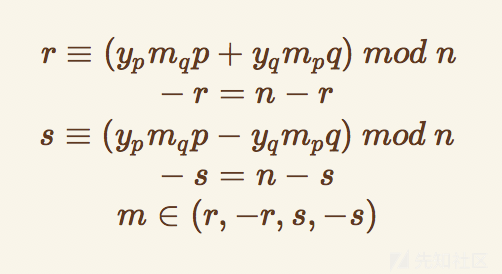
小性质
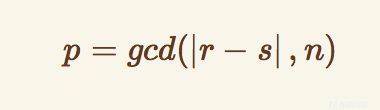
计算脚本
import gmpy2
import string
from Crypto.PublicKey import RSA
with open('pubkey.pem', 'r') as f:
key = RSA.importKey(f)
N = key.n
e = key.e
with open('flag.enc', 'r') as f:
cipher = f.read().encode('hex')
cipher = string.atoi(cipher, base=16)
q = ......
p = ......
inv_p = gmpy2.invert(p, q)
inv_q = gmpy2.invert(q, p)
mp = pow(cipher, (p + 1) / 4, p)
mq = pow(cipher, (q + 1) / 4, q)
a = (inv_p * p * mq + inv_q * q * mp) % N
b = N - int(a)
c = (inv_p * p * mq - inv_q * q * mp) % N
d = N - int(c)
for i in (a, b, c, d):
s = '%x' % i
if len(s) % 2 != 0:
s = '0' + s
print s.decode('hex')
低指数攻击
满足条件
e很小,通常为3
通解方法
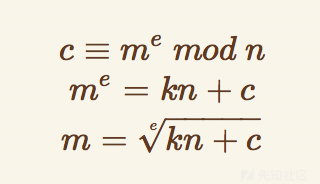
当e很小的时候,我们爆破k,开e次方即可得到m
计算脚本
import gmpy
import libnum
from Crypto.Util import number
import gmpy2
def getd(e,p,q):
phi = (p - 1) * (q - 1)
d = gmpy2.invert(e, phi) % phi
return d
def getm(m):
return int(m.encode('hex'), 16)
c=....
n=....
e=3
i = 0
while 1:
if (gmpy.root(c + i * n, 3)[1] == 1):
m = gmpy.root(c + i * n, 3)[0]
print libnum.n2s(m)
break
i = i + 1
低指数广播攻击
满足条件
当有如下条件

我们有多组(c,n),但是他们都是用同样的公钥加密同样的消息,且这里的公钥是一个低指数
通解方法
此时就可以使用中国剩余定理计算通解

其中
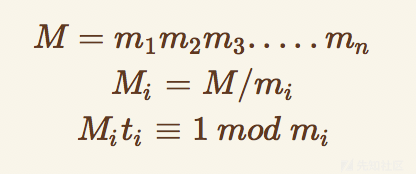
详细链接
http://skysec.top/2018/09/13/Crypto-RSA多等式攻击总结/#多等式之低加密指数广播攻击计算脚本
脚本如下
import gmpy2
import gmpy
import libnum
question = [c1,c2,c3....n1,n2,n3...]
N = 1
e=10
for i in range(len(question)):
N*=question[i]['n']
N_list = []
for i in range(len(question)):
N_list.append(N/question[i]['n'])
t_list = []
for i in range(len(question)):
t_list.append(int(gmpy2.invert(N_list[i],question[i]['n'])))
sum = 0
for i in range(len(question)):
sum = (sum+question[i]['c']*t_list[i]*N_list[i])%N
sum = gmpy.root(sum,e)[0]
print libnum.n2s(sum)
Related Message Attack
满足条件
当e=3时,我们有如下条件

此时,我们有(c1,c2,n,padding)的值
通解方法
那么就可以使用此攻击,得到通解

详细推导过程见
http://skysec.top/2018/09/15/浅析RSA-Padding-Attack/计算脚本
脚本如下
def getM2(a,b,c1,c2,n):
a3 = pow(a,3,n)
b3 = pow(b,3,n)
first = c1-a3*c2+2*b3
first = first % n
second = 3*b*(a3*c2-b3)
second = second % n
third = second*gmpy2.invert(first,n)
third = third % n
fourth = (third+b)*gmpy2.invert(a,n)
return fourth % n
m = getM2(a,b,c1,c2,n)-padding2
print libnum.n2s(m)
Winner's Attack
满足条件
当题目中
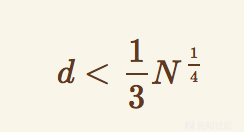
那么即可使用Winner's Attack
更简单的判断方式为:e很大
计算脚本
https://github.com/pablocelayes/rsa-wiener-attackBoneh and Durfee attack
满足条件
当题目中
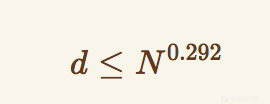
那么即可使用Boneh and Durfee attack
更简单的判断方式为:e很大,且Winner's Attack无法使用
计算脚本
https://github.com/mimoo/RSA-and-LLL-attacks与Winner's Attack对比
Boneh and Durfee attack的条件需求比Winner's Attack的需求低的多
所以一般情况下,在e很大的情况下,Winner's Attack无法使用可以使用Boneh and Durfee attack