前言

今天主要是分析一下在攻击椭圆曲线时应用的Pollard Rho算法，一般来讲这在针对ECDLP的攻击方法里算是比较有效的，对于一般的应用中的椭圆曲线都能起到作用，另一种针对普通的椭圆曲线也较为有效的算法就是Pohlig-Hellman了，这个如果不清楚的话也可参考我写的文章，简析ECC攻击方法之Pohlig-Hellman，在里面也对椭圆曲线的离散对数问题即ECDLP做了简要介绍

Pollard Rho算法的主要思想

就我目前了解的来看Pollard Rho算法应该都构成一个体系了，它其实是一种随机性的概率型算法，基于PR算法我们可以加速大整数的因子分解，这也是1975年Pollard提出该算法时的应用方面，这可以用来攻击RSA的公钥密码体制，之后在1978年Pollard又利用循环群ρ形的特点提出了用于解决离散对数问题的PR算法，后来也扩展到了椭圆曲线上，这样PR算法便成功威胁到了整个公钥密码体系，Pollard真的是很厉害

Pollard Rho算法中所利用的一大技巧应该就是生日悖论了，这个我想大家应该也都有所了解，就是我们取k个学生时这些学生里至少有两个人的生日在同一天的概率会是多大，从直觉上讲要取得较高的概率我们可能会觉得需要取很多人，然而事实上只需要取1.2*N^(1/2)也就是1.2*365^(1/2)，大约为23时就可以使概率提高到50%，当取到58人时概率就已经达到了99%，几乎可以肯定会有两个生日在同一天的人出现，这确实是挺奇妙的，所以刚认识这个算法你可能会觉得违反认知，所以它被称作是一个悖论

关于这一技巧我感觉在应用于整数的因子分解的Pollard算法中比较明显，具体可以参考这篇翻译文章Pollard-rho算法详解，写的确实非常好，本来还想讲两句，不过这里面已经讲得很通俗了，就不多说了

至于解决离散对数问题的Pollard Rho算法，确实是有点难，它可以帮助我们在有限的循环群上解决离散对数问题

简单来看我们取一个大素数P，设G为一个乘法的循环群，其生成元为g，则该群的阶就是N=P-1

此时在G上的离散对数问题就是对于G中的元素q，找到x使得g^x=q，而Pollard Rho算法主要就是利用了循环群的生成序列呈现一个ρ字形状，就像下面这样，设Rj为循环群中的元素

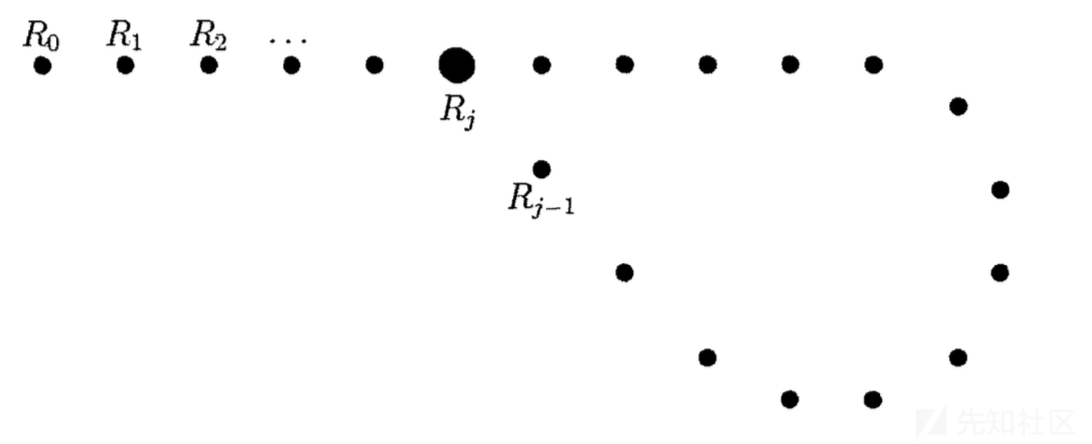
然后我们需要判断我们求的元素是否在这个图形中的环上，如果在环上我们就可以利用周期性来解决离散对数问题，前面我们也提到了PR算法是一个概率性算法，这里我们构造序列时也是随机生成的，思想上应该说也是利用了生日悖论问题

用Pollard Rho解决ECDLP的过程

首先设定一个ECDLP问题，对于椭圆曲线E(Fp)，我们取基点P，且P的阶为N，然后对于曲线上另一点Q，我们需要求k，使得P*k=Q

使用Pollard Rho算法，过程如下

1. 我们令G=E(Fp)，然后我们将G分成三个大小相近的部分S1,S2,S3，这里可以利用hash函数进行选择
2. 然后我们设定一个用于生成随机的步数的迭代函数f：
   
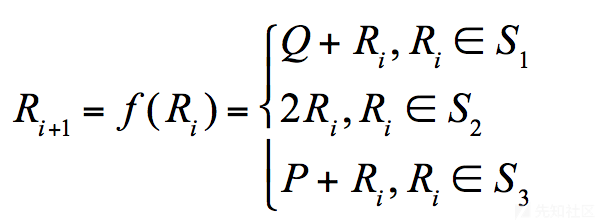
3. 接下来我们令Ri = aiP+biQ，则有：
   
4. 然后我们初始化参数，取R0=P，a0=1，b0=0，然后不断生成配对(Ri,R2i)，直到我们找到了某个m，有Rm=R2m，则有：
   

这里在最后求k时会涉及模反，也就是要对元素求逆，而满足求逆条件则此处的分母bm-b2m需满足gcd(bm-b2m,n)=1，否则将无法求得k，所以有些时候Pollard Rho算法也是不起作用的，但是一般情况下我们选择的椭圆曲线的阶N都是含有大的素因子的，这也是为了抵抗 Pohlig-Hellman攻击，但这种情况正好满足了Pollard Rho的攻击条件 ，所以在实际应用中一般都是可以奏效的

使用Pollard Rho算法后我们成功将求解的时间复杂度降到了O(√N)，至于空间复杂度则可以忽略不计，因为该算法是个概率型算法，每次只随机选取一对进行比较，所以不会占用存储，这与大步小步算法相反，其实PR算法也可以看作是大步小步算法的随机化版本，继承令时间复杂度的有点，同时还减少了空间的消耗，因为大步小步算法需要占用大量的存储空间

当然了，这里所讲的也只是一个简单的Pollard Rho运算过程，实际的应用里还有很多要调整的，就我们上面的算法过程而言，对与不同的椭圆曲线能命中的概率与效率也是不同的，这取决于我们设定的迭代函数以及我们初始化的点位，所以在实际的应用里往往需要针对特定的椭圆曲线设定特定的迭代函数以及初始化参数，有时候初始化参数没选好可能就把点定到ρ形循环序列的环外去了，另外还可以将PR算法并行运算以获得更好的效果，具体的这里就不多说了(因为我也不会)，不是专门搞这方面研究的话也没必要做的这么深入，下面我们简单地在工程上实践一下

简单实践

这里本来是想找一道ctf题目来讲讲，不过暂时没找到难度比较合适的，国外的题目让我有点懵逼，以前也没怎么打crypto的题目，所以也没存，在这我就简单求解一个ECDLP

用到的工具还是sagemath，现在越来越感觉这是个神器了，之前使用Pohlig-Hellman算法也是在这里面直接用的函数，这次，里面也很贴心的帮你封装了PR算法

首先我们选定一个椭圆曲线，这里我们先挑选一个简单的曲线进行演示

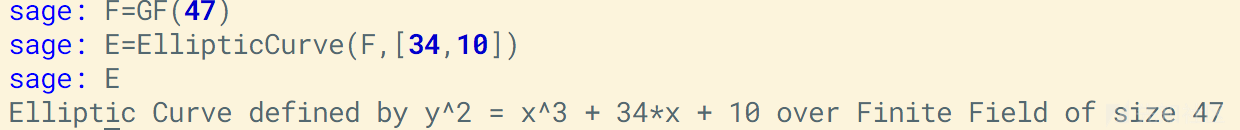
然后我们选择基点P，并求得它的阶N，即此处的order，接下来选择一个Q点，这里我们设定k为14

然后调用sagemath封装的discrete_log_rho函数即可求得k

这里P的阶恰好是素数，如果不是素数我们需要将其阶分解然后将P,Q乘上除大素数外的因子对阶进行转变，否则就如我们前面所提到的，这个算法是跑不起来的，在sagemath里还有很多很多其他的算法，因为它实际上是一百多个数学工具库的集合，用好了也非常牛b，只是可惜国内资料较少，只能头疼地翻文档

写在最后

最近这一段时间的学习可以说是让我充分领略到了数学的魅力，不过确实是很难，想要看懂很多概念还得不断提高自己的姿势水平，还是要一直学习啊，另外因为水平有限，文章可能存在一些纰漏，还请师傅们多多指教