前言

本篇是Cryptography密码学类的题解。难度从简到难，涉及了一些ctf比赛中常见的密码学套路。部分题目附件已打包。
链接: https://pan.baidu.com/s/13LVIkBMuUekRLGCsLElIVg 提取码: 3ei6

Crypto Warmup 1

Question

Crpyto can often be done by hand, here's a message you got from a friend, llkjmlmpadkkc with the key of thisisalilkey. Can you use this table to solve it?.

Hint

Submit your answer in our competition's flag format. For example, if you answer was 'hello', you would submit 'picoCTF{HELLO}' as the flag.

Please use all caps for the message.

Solution

维吉尼亚密码，详细内容可以参考wiki。解密脚本如下：

#!/usr/bin/env python
# -*- coding: utf-8 -*-


cipher = 'llkjmlmpadkkc'
key = 'thisisalilkey'
message = ''


for i in xrange(len(cipher)):
    message += chr(((ord(cipher[i]) - 97) - (ord(key[i]) - 97) + 26) % 26 + 97)

print message

flag:picoCTF{SECRETMESSAGE}

Crypto Warmup 2

Question

Cryptography doesn't have to be complicated, have you ever heard of something called rot13? cvpbPGS{guvf_vf_pelcgb!}

Hint

This can be solved online if you don't want to do it by hand!

Solution

凯撒密码，经过一次rot13就可以恢复原文。

❯ python -c "print 'cvpbPGS{guvf_vf_pelcgb!}'.decode('rot_13')"
picoCTF{this_is_crypto!}

flag:picoCTF{this_is_crypto!}

HEEEEEEERE'S Johnny!

Question

Okay, so we found some important looking files on a linux computer. Maybe they can be used to get a password to the process. Connect with nc 2018shell1.picoctf.com 5221. Files can be found here: passwd shadow.

Hint

If at first you don't succeed, try, try again. And again. And again.

If you're not careful these kind of problems can really "rockyou".

Solution

根据题目名字提示，可以使用John the Ripper，一款密码破解工具。使用john自带的密码表就可以跑出root的密码了。

❯ ./unshadow passwd shadow > ./crack.db
❯ ./john ./crack.db
Warning: detected hash type "sha512crypt", but the string is also recognized as "sha512crypt-opencl"
Use the "--format=sha512crypt-opencl" option to force loading these as that type instead
Warning: hash encoding string length 98, type id $6
appears to be unsupported on this system; will not load such hashes.
Loaded 1 password hash (sha512crypt, crypt(3) $6$ [SHA512 64/64 OpenSSL])
Press 'q' or Ctrl-C to abort, almost any other key for status
kissme           (root)
1g 0:00:00:06 DONE 2/3 (2018-10-14 11:56) 0.1529g/s 361.6p/s 361.6c/s 361.6C/s kissme
Use the "--show" option to display all of the cracked passwords reliably
Session completed
❯ nc 2018shell2.picoctf.com 40157
Username: root
Password: kissme
picoCTF{J0hn_1$_R1pp3d_1b25af80}

flag:picoCTF{J0hn_1$_R1pp3d_1b25af80}

caesar cipher 1

Question

This is one of the older ciphers in the books, can you decrypt the message? You can find the ciphertext in /problems/caesar-cipher-1_4_e4dc6dcfb004bdade0b9ce8e44f1bac4 on the shell server.

Hint

caesar cipher tutorial

Solution

还是凯撒，爆破一下偏移量，找到有意义的字符串。

#!/usr/bin/env python
# -*- coding: utf-8 -*-


cipher = 'vgefmsaapaxpomqemdoubtqdxoaxypeo'
for j in xrange(25):
    flag = ''
    for i in cipher:
        if ord(i) >= 97 and ord(i) <= 122:
            flag += chr(((ord(i) - 97) + j) % 26 + 97)
        if ord(i) >= 65 and ord(i) <= 91:
            flag += chr(((ord(i) - 65) + j + 26) % 26 + 65)
    print flag

结果如下：

vgefmsaapaxpomqemdoubtqdxoaxypeo
whfgntbbqbyqpnrfnepvcureypbyzqfp
xighouccrczrqosgofqwdvsfzqczargq
yjhipvddsdasrpthpgrxewtgardabshr
zkijqweetebtsquiqhsyfxuhbsebctis
aljkrxffufcutrvjritzgyvictfcdujt
bmklsyggvgdvuswksjuahzwjdugdevku
cnlmtzhhwhewvtxltkvbiaxkevhefwlv
domnuaiixifxwuymulwcjbylfwifgxmw
epnovbjjyjgyxvznvmxdkczmgxjghynx
fqopwckkzkhzywaownyeldanhykhizoy
grpqxdllaliazxbpxozfmeboizlijapz
hsqryemmbmjbaycqypagnfcpjamjkbqa
itrszfnncnkcbzdrzqbhogdqkbnklcrb
justagoodoldcaesarcipherlcolmdsc
kvtubhppepmedbftbsdjqifsmdpmnetd
lwuvciqqfqnfecguctekrjgtneqnofue
mxvwdjrrgrogfdhvduflskhuofropgvf
nywxeksshsphgeiwevgmtlivpgspqhwg
ozxyflttitqihfjxfwhnumjwqhtqrixh
payzgmuujurjigkygxiovnkxriursjyi
qbzahnvvkvskjhlzhyjpwolysjvstkzj
rcabiowwlwtlkimaizkqxpmztkwtulak
sdbcjpxxmxumljnbjalryqnaulxuvmbl
tecdkqyynyvnmkockbmszrobvmyvwncm

找到有意义的字符串justagoodoldcaesarcipherlcolmdsc，得到flag。

flag:picoCTF{justagoodoldcaesarcipherlcolmdsc}

hertz

Question

Here's another simple cipher for you where we made a bunch of substitutions. Can you decrypt it? Connect with nc 2018shell1.picoctf.com 18581.

Hint

NOTE: Flag is not in the usual flag format

Solution

替换密码，因为给的段落足够长，所以可以对词频进行静态分析，得到替换表，然后恢复原文，在线工具。

flag:substitution_ciphers_are_solvable_fuosdblgwv

blaise's cipher

Question

My buddy Blaise told me he learned about this cool cipher invented by a guy also named Blaise! Can you figure out what it says? Connect with nc 2018shell1.picoctf.com 46966.

Hint

There are tools that make this easy.

This cipher was NOT invented by Pascal

Solution

还是关于维吉尼亚密码（发明者全名为Blaise De Vigenère），和第一题不同的是这题没有提供密钥。但这题给的密文还是相当的长，依然可以使用静态分析，主要的方法有Kasiski 测试法和互重合指数法。这里使用https://www.mygeocachingprofile.com/codebreaker.vigenerecipher.aspx做分析。

得到密钥：flag。

然后解密，得到flag。

flag:picoctf{v1gn3r3_c1ph3rs_ar3n7_bad_cdf08bf0}

hertz 2

Question

This flag has been encrypted with some kind of cipher, can you decrypt it? Connect with nc 2018shell1.picoctf.com 23479.

Hint

These kinds of problems are solved with a frequency that merits some analysis.

Solution

还是替换密码，不过这次给的密文比较短。

Let's decode this now!
Jea vbpkh glsni dsc obmyf stal jea wqzx usr. P kqi'j gawpata jepf pf fbke qi aqfx ylsgwam pi Ypks. Pj'f qwmsfj qf pd P fswtau q ylsgwam qwlaqux! Shqx, dpia. Eala'f jea dwqr: ypksKJD{fbgfjpjbjpsi_kpyealf_qla_jss_aqfx_txugsyxgti}

根据flag的特征，可以得到线索ypksKJD=picoCTF。再使用https://quipqiup.com/，设置线索进行破解。

flag:picoCTF{substitution_ciphers_are_too_easy_vydbopybvn}

Safe RSA

Question

Now that you know about RSA can you help us decrypt this ciphertext? We don't have the decryption key but something about those values looks funky..

Hint

RSA tutorial)

Hmmm that e value looks kinda small right?

These are some really big numbers.. Make sure you're using functions that don't lose any precision!

Solution

附件给了密文和公钥对：

N: 374159235470172130988938196520880526947952521620932362050308663243595788308583992120881359365258949723819911758198013202644666489247987314025169670926273213367237020188587742716017314320191350666762541039238241984934473188656610615918474673963331992408750047451253205158436452814354564283003696666945950908549197175404580533132142111356931324330631843602412540295482841975783884766801266552337129105407869020730226041538750535628619717708838029286366761470986056335230171148734027536820544543251801093230809186222940806718221638845816521738601843083746103374974120575519418797642878012234163709518203946599836959811
e: 3

ciphertext (c): 2205316413931134031046440767620541984801091216351222789180593875373829950860542792110364325728088504479780803714561464250589795961097670884274813261496112882580892020487261058118157619586156815531561455215290361274334977137261636930849125

e很明显太小了，存在低加密指数攻击，详细可以参考CTF中RSA的常见攻击方法。

也就是说加密时，如果明文的三次方依然小于N，会导致mod N这一步根本没有用到，直接对密文三次开方即可得到明文。

即：

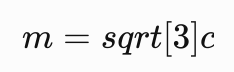
如果明文的三次方比n大，但并不是很大，那么设k，存在以下关系：

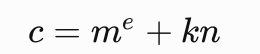
爆破k，如果

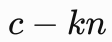
能开三次根式，那么可以直接得到明文。

爆破脚本：

import gmpy

N = 374159235470172130988938196520880526947952521620932362050308663243595788308583992120881359365258949723819911758198013202644666489247987314025169670926273213367237020188587742716017314320191350666762541039238241984934473188656610615918474673963331992408750047451253205158436452814354564283003696666945950908549197175404580533132142111356931324330631843602412540295482841975783884766801266552337129105407869020730226041538750535628619717708838029286366761470986056335230171148734027536820544543251801093230809186222940806718221638845816521738601843083746103374974120575519418797642878012234163709518203946599836959811
e = 3

c = 2205316413931134031046440767620541984801091216351222789180593875373829950860542792110364325728088504479780803714561464250589795961097670884274813261496112882580892020487261058118157619586156815531561455215290361274334977137261636930849125


i = 0
while 1:
    if(gmpy.root(c + i * N, 3)[1] == 1):
        print gmpy.root(c + i * N, 3),i
        break
    i = i + 1
d = hex(13016382529449106065839070830454998857466392684017754632233929110204433151964285)
print d[2:-1].decode('hex')

flag:picoCTF{e_w4y_t00_sm411_9f5d2464}

caesar cipher 2

Question

Can you help us decrypt this message? We believe it is a form of a caesar cipher. You can find the ciphertext in /problems/caesar-cipher-2_3_4a1aa2a4d0f79a1f8e9a29319250740a on the shell server.

Hint

You'll have figure out the correct alphabet that was used to encrypt the ciphertext from the ascii character set

ASCII Table

Solution

加入了特殊字符的凯撒密码，爆破范围从大小写字母扩大到所有可能的偏移量。脚本如下：

#!/usr/bin/env python
# -*- coding: utf-8 -*-


cipher = '^WQ]1B4iQ/SaO@M1W>V3`AMXcABMO@3\\BMa3QC`3k'
for j in xrange(0,126):
    flag = ''
    for i in cipher:
        flag += chr((ord(i)  + j))
    print flag

flag:picoCTF{cAesaR_CiPhErS_juST_aREnT_sEcUrE}

rsa-madlibs

Question

We ran into some weird puzzles we think may mean something, can you help me solve one? Connect with nc 2018shell1.picoctf.com 40440

Hint

RSA info

Solution

nc连接服务器，需要根据描述一步步的解决关于RSA加解密的问题：

❯ nc 2018shell1.picoctf.com 40440
0x7069636f4354467b64305f755f6b6e30775f7468335f7740795f325f5253405f35643338336531307dL <type 'long'>
Hello, Welcome to RSA Madlibs
Keeping young children entertained, since, well, nev3r
Tell us how to fill in the blanks, or if it's even possible to do so
Everything, input and output, is decimal, not hex
#### NEW MADLIB ####
q : 93187
p : 94603
##### WE'RE GONNA NEED THE FOLLOWING ####
n
IS THIS POSSIBLE and FEASIBLE? (Y/N):

可以双开窗口，边解边答。只要我的手速够快，服务器断线的速度就跟不上我-0-。

不过不知道开头为什么给了一串16进制字符串，解一下直接得到了flag……

❯ python -c "print('7069636f4354467b64305f755f6b6e30775f7468335f7740795f325f5253405f35643338336531307d').decode('hex')"
picoCTF{d0_u_kn0w_th3_w@y_2_RS@_5d383e10}

flag:picoCTF{d0_u_kn0w_th3_w@y_2_RS@_5d383e10}

SpyFi

Question

James Brahm, James Bond's less-franchised cousin, has left his secure communication with HQ running, but we couldn't find a way to steal his agent identification code. Can you? Conect with nc 2018shell1.picoctf.com 30399. Source.

Hint

What mode is being used?

Solution

查看程序源码，使用的是AES的ECB模式，padding为16位：

...
def pad(message):
    if len(message) % 16 != 0:
        message = message + '0' * (16 - len(message) % 16)
    return message


def encrypt(key, plain):
    cipher = AES.new(key.decode('hex'), AES.MODE_ECB)
    return cipher.encrypt(plain).encode('hex')
...

AES-ECB模式的加解密方式如图：

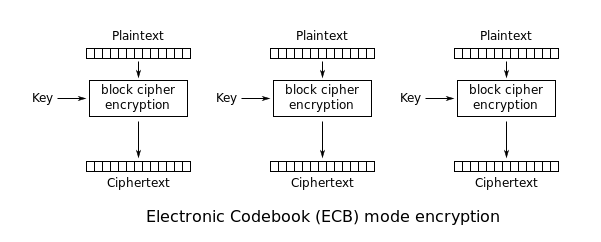
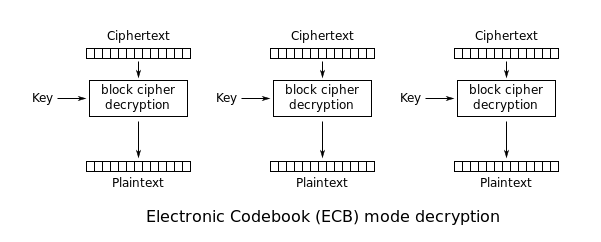
再看程序中默认会发送的字符串：

...
welcome = "Welcome, Agent 006!"
print welcome

sitrep = raw_input("Please enter your situation report: ")
message = """Agent,
Greetings. My situation report is as follows:
{0}
My agent identifying code is: {1}.
Down with the Soviets,
006
""".format(sitrep, agent_code)

message = pad(message)
print encrypt("""key""", message)
...

我们向服务器发送AAAAAAAAAAA + BBBBBBBBBBBBBBBB + CCCCCCCCCCCCCCCC，共11个A，16个B和C。

假设flag为16位的picoCTF{1234567}，那么服务器接收到的字符串就会类似如下的形式：

'Agent,\nGreetings'   (块 1)
   '. My situation r'    (块 2)
   'eport is as foll'    (块 3)
   'ows:\nAAAAAAAAAAA'   (块 4)
   'BBBBBBBBBBBBBBBB'    (块 5)
   'CCCCCCCCCCCCCCCC'    (块 6)
   '\nMy agent identi'   (块 7)
   'fying code is:  '    (块 8)  <--- 已知
   'picoCTF{1234567}'    (块 9)  <--- 未知
   '.Down with the S'    (块 10) <--- 已知

接着，少发送一个C，就会变成

'Agent,\nGreetings'   (块 1)
   '. My situation r'    (块 2)
   'eport is as foll'    (块 3)
   'ows:\nAAAAAAAAAAA'   (块 4)
   'BBBBBBBBBBBBBBBB'    (块 5)
   'CCCCCCCCCCCCCCC\n'   (块 6)
   'My agent identif'    (块 7)
   'ying code is:  p'    (块 8)  <--- 在这里我们得到了包含flag第一位的密文，但并不知道第一位具体是什么
   'icoCTF{1234567}.'    (块 9)  <--- 未知
   'Down with the So'    (块 10) <--- 已知

把块 5替换成块 8的格式化输入

'Agent,\nGreetings'   (块 1)
   '. My situation r'    (块 2)
   'eport is as foll'    (块 3)
   'ows:\nAAAAAAAAAAA'   (块 4)
   'ying code is: %s'    (块 5)  <--- 可以逐位爆破%s
   'CCCCCCCCCCCCCCC\n'   (块 6)
   'My agent identif'    (块 7)
   'ying code is:  p'    (块 8)  <--- 在这里我们得到了包含flag第一位的密文，但并不知道这个密文是什么
   'icoCTF{1234567}.'    (块 9)  <--- 未知
   'Down with the So'    (块 10) <--- 已知

爆破块 5，如果密文和块 8相同，则表示我们找到了flag的第一位，接下来，再减少一个C，使得块 8带有flag的前两位字符。如下：

'Agent,\nGreetings'   (块 1)
   '. My situation r'    (块 2)
   'eport is as foll'    (块 3)
   'ows:\nAAAAAAAAAAA'   (块 4)
   'ing code is: p%s'    (块 5)  <--- 同步替换块 5
   'CCCCCCCCCCCCCC\nM'   (块 6)
   'y agent identify'    (块 7)
   'ing code is:  pi'    (块 8)  <--- 包含flag第一、二位的密文
   'coCTF{1234567}.D'    (块 9)  <--- 未知
   'own with the Sov'    (块 10) <--- 已知

然后继续爆破flag的第二位。依次循环下去，就可以获得完整的flag。

爆破脚本如下(服务器加密一次后就会断开连接，所以跑完flag所用的时间会比较长)：

#!/usr/bin/env python
# -*- coding: utf-8 -*-


from pwn import * 
flag = "picoCTF{"

for j in range(1,14):
   p = remote('2018shell1.picoctf.com', 30399)
   p.recvuntil('Please enter your situation report: ')
   my_msg = "A"*11+"B"*(25-j)
   p.sendline(my_msg)
   enc_msg = p.recv(1024).decode('hex')
   p.close()

   for i in range(32,128):
       q = remote('2018shell1.picoctf.com', 30399)
       q.recvuntil('Please enter your situation report: ')
       msg = "A"*11+"B"*(14-j) + flag + chr(i)

       q.sendline(msg)
       y = q.recv(1024).decode('hex')
       q.close()
       if y[80:96] == enc_msg[128:144]:
           flag += chr(i)
           break
print(flag)

flag:picoCTF{@g3nt6_1$_th3_c00l3$t_2432504}

Super Safe RSA

Question

Dr. Xernon made the mistake of rolling his own crypto.. Can you find the bug and decrypt the message? Connect with nc 2018shell1.picoctf.com 6262.

Hint

Just try the first thing that comes to mind.

Solution

看一下信息：

c: 6075087024476414532659138701716437603217113412924927299863787548188620337158625
n: 16995743251555690273217604748218275023627813110906708466533535245776011465591891
e: 65537

n很小，总共才80位，可以使用爆破的方式解出p和q
。在线工具
。

得到结果：

p = 166402962209062256362900394698423820317
q = 102136061918194068640310910627905419563823

然后就是很简单的rsa解密了。

from Crypto.Util.number import inverse
p = 166402962209062256362900394698423820317
q = 102136061918194068640310910627905419563823
c = 6075087024476414532659138701716437603217113412924927299863787548188620337158625
n = 16995743251555690273217604748218275023627813110906708466533535245776011465591891
e = 65537

phi = (q-1)*(p-1)
d = inverse(e, phi)
print (hex(pow(c,d,n))[2:-1]).decode('hex')

得到flag。

flag:picoCTF{us3_l@rg3r_pr1m3$_2461}

Super Safe RSA 2

Question

Wow, he made the exponent really large so the encryption MUST be safe, right?! Connect with nc 2018shell1.picoctf.com 56543.

Hint

What is the usual value for e?

Solution

nc连接服务器，发现这回e的值不小了，但是又变得和N差不多大了，还是参考CTF中RSA的常见攻击方法，这里存在低解密指数攻击。

Wiener表示如果满足：

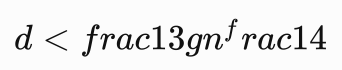
那么一种基于连分数(一个数论当中的问题)的特殊攻击类型就可以危害RSA的安全。此时需要满足：

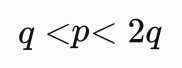
如果满足上述条件，通过Wiener Attack可以在多项式时间中分解n。

使用开源工具https://github.com/pablocelayes/rsa-wiener-attack

'''
Created on Dec 14, 2011

@author: pablocelayes
'''

import ContinuedFractions, Arithmetic, RSAvulnerableKeyGenerator

def hack_RSA(e,n):
    '''
    Finds d knowing (e,n)
    applying the Wiener continued fraction attack
    '''
    frac = ContinuedFractions.rational_to_contfrac(e, n)
    convergents = ContinuedFractions.convergents_from_contfrac(frac)

    for (k,d) in convergents:

        #check if d is actually the key
        if k!=0 and (e*d-1)%k == 0:
            phi = (e*d-1)//k
            s = n - phi + 1
            # check if the equation x^2 - s*x + n = 0
            # has integer roots
            discr = s*s - 4*n
            if(discr>=0):
                t = Arithmetic.is_perfect_square(discr)
                if t!=-1 and (s+t)%2==0:
                    print("Hacked!")
                    return d

if __name__ == "__main__":
    print hack_RSA(40276660093351912353325027146420685937733052504816262053896184883506171821807404583368346339215117527771791856465371395445756580309600483928576564180890942975279324690215478497697070066763075254913358736488880708349691537688815542401252154948245178131989398664206152846321309331764046013649756619261071229089, 111583170127578807909192691245137491304582814592836631984536450317481568426014198265987965591526088832329215543505708705754504100598169044438075849117477605468201110960653836265368253728288600909205172996903271308132928634087380939250941030896277683335203499540010766665619316042268962892586456274440478367001)

解得私钥d：65537，然后解密：

from Crypto.Util.number import inverse
c = 85669272593914592964238296252223602553240367010559050180727431963691933620008524312226679252731896404760784512941433411361850153756503392392692524466402024374178583928667263379044625258718935929469661451158056304059057475244237032774703099421851155804449755624009586256845110664849184621665767806044750594973
n = 111583170127578807909192691245137491304582814592836631984536450317481568426014198265987965591526088832329215543505708705754504100598169044438075849117477605468201110960653836265368253728288600909205172996903271308132928634087380939250941030896277683335203499540010766665619316042268962892586456274440478367001
e = 40276660093351912353325027146420685937733052504816262053896184883506171821807404583368346339215117527771791856465371395445756580309600483928576564180890942975279324690215478497697070066763075254913358736488880708349691537688815542401252154948245178131989398664206152846321309331764046013649756619261071229089
d = 65537
m = pow(c, d, n)
print hex(m)[2:-1].decode('hex')

flag:picoCTF{w@tch_y0ur_Xp0n3nt$_c@r3fu11y_5261983}

Super Safe RSA 3

Question

The more primes, the safer.. right.?.? Connect with nc 2018shell1.picoctf.com 11423.

Hint

How would you find d if there are more than 2 prime factors of n?

Solution

这题给我们的数据如下：

c: 2214959746368961374343866619773680463913808855252144119575578619282028038148568609891198127966225495311682540323131579203618894145626046974546075970616339033486317429461235324910794466410074881752239541146624247745072518241741204968025293372054661473208051944193745386532992238774551013797836031291096741
n: 5564465787507426784189854287795264081761345977763964262369153883931335062166838686916377911069328789715623668583315372050520387414170383621534793892389463905512682152442890656361180400315699526374103389751180954335677791471685242043876553878553597343813515063304714971565013966010693181624796612216036537
e: 65537

使用Alpertron分解，n可以分解为多个质因子。

解密过程可以参考https://crypto.stackexchange.com/questions/31109/rsa-enc-decryption-with-multiple-prime-modulus-using-crt。

脚本如下：

c = 2214959746368961374343866619773680463913808855252144119575578619282028038148568609891198127966225495311682540323131579203618894145626046974546075970616339033486317429461235324910794466410074881752239541146624247745072518241741204968025293372054661473208051944193745386532992238774551013797836031291096741

n = 5564465787507426784189854287795264081761345977763964262369153883931335062166838686916377911069328789715623668583315372050520387414170383621534793892389463905512682152442890656361180400315699526374103389751180954335677791471685242043876553878553597343813515063304714971565013966010693181624796612216036537

e = 65537

p1 = 2175350609
p2 = 2182560491
p3 = 2196605027
p4 = 2209029391
p5 = 2466547367
p6 = 2510616961
p7 = 2588079563
p8 = 2704140821
p9 = 2736762829
p10 = 2796597043
p11 = 2809479437
p12 = 2829659713
p13 = 2837556643
p14 = 2858051057
p15 = 3032087491
p16 = 3042267581
p17 = 3063304267
p18 = 3102491383
p19 = 3219243151
p20 = 3284737447
p21 = 3392021827
p22 = 3789952469
p23 = 3812358577
p24 = 3858988619
p25 = 3864352469
p26 = 3877179469
p27 = 3910354507
p28 = 3985847791
p29 = 3990903569
p30 = 4041031661
p31 = 4069378073
p32 = 4203209281

primes = [p1, p2, p3, p4, p5, p6, p7, p8, p9, p10, p11, p12, p13, \
          p14, p15, p16, p17, p18, p19, p20, p21, p22, p23, p24, p25, \
          p26, p27, p28, p29, p30, p31, p32]

def egcd(a, b):
    if a == 0:
        return (b, 0, 1)
    else:
        g, y, x = egcd(b % a, a)
        return (g, x - (b // a) * y, y)

def modinv(a, m):
    g, x, y = egcd(a, m)
    if g != 1:
        raise Exception('modular inverse does not exist')
    else:
        return x % m


# From https://crypto.stackexchange.com/questions/31109/rsa-enc-decryption-with-multiple-prime-modulus-using-crt
ts = []
xs = []
ds = []

for i in range(len(primes)):
    ds.append(modinv(e, primes[i]-1))

m = primes[0]

for i in range(1, len(primes)):
    ts.append(modinv(m, primes[i]))
    m = m * primes[i]

for i in range(len(primes)):
    xs.append(pow((c%primes[i]), ds[i], primes[i]))

x = xs[0]
m = primes[0]

for i in range(1, len(primes)):
    x = x + m * ((xs[i] - x % primes[i]) * (ts[i-1] % primes[i]))
    m = m * primes[i]


print hex(x%n)[2:-1].decode("hex")

flag:picoCTF{p_&*q_n0_r*$_t!!_6725536}

picoCTF2018 Writeup之Cryptography篇

前言

Crypto Warmup 1

Question

Hint

Solution

Crypto Warmup 2

Question

Hint

Solution

HEEEEEEERE'S Johnny!

Question

Hint

Solution

caesar cipher 1

Question

Hint

Solution

hertz

Question

Hint

Solution

blaise's cipher

Question

Hint

Solution

hertz 2

Question

Hint

Solution

Safe RSA

Question

Hint

Solution

caesar cipher 2

Question

Hint

Solution

rsa-madlibs

Question

Hint

Solution

SpyFi

Question

Hint

Solution

Super Safe RSA

Question

Hint

Solution

Super Safe RSA 2

Question

Hint

Solution

Super Safe RSA 3

Question

Hint

Solution

Hacking more